Revisiting Needs and Interfaces with Generative AI

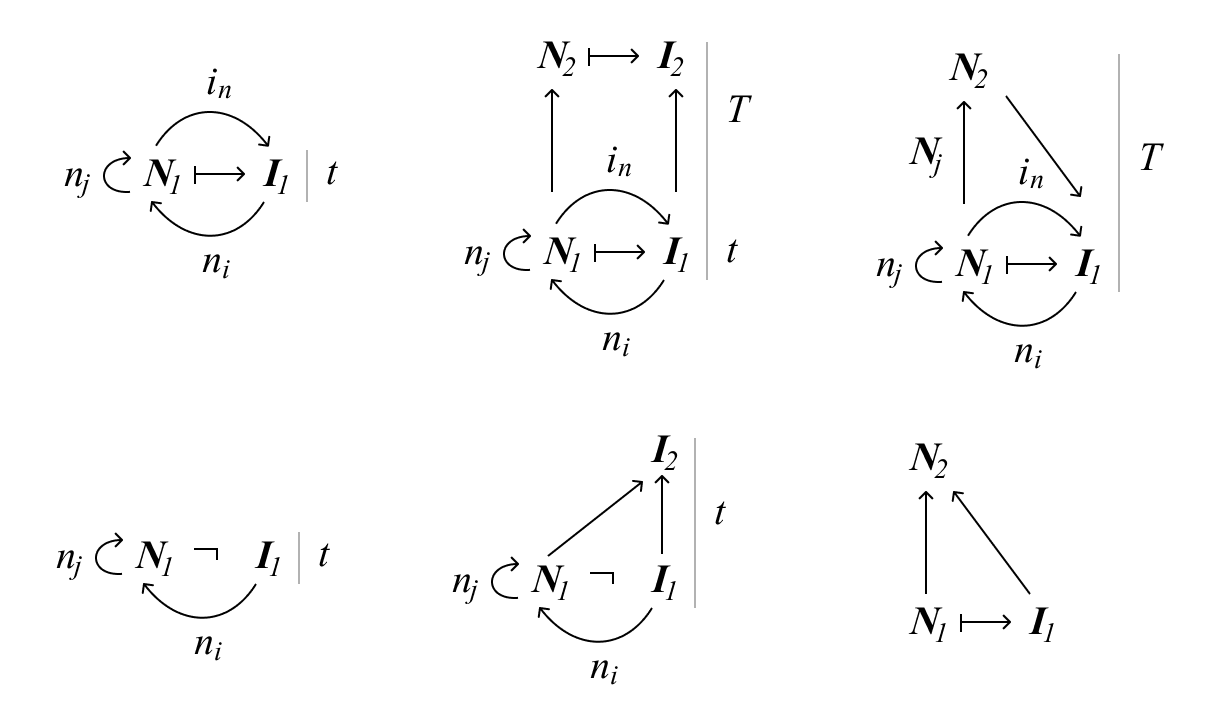
Preface

Inspired by Terence Tao's talk on the potential for AI in science and mathematics, I’m revisiting my original essay, Needs and Interfaces, in collaboration with ChatGPT. This revision is both an intellectual exploration and a philosophical experiment—a stress test of human-AI collaboration on an esoteric topic. Why involve AI? Because, as with design itself, the evolving nature of human-AI relationships reflects our shifting understanding of tools and technology. Drawing on Heidegger’s philosophy of the tool, where tools becomes an extension of human existence, this essay aims to examine how AI can augment human thought in the context of design. Before proceeding, I urge you to read the original essay, as this revision builds on those ideas and may otherwise seem nonsensical.

As someone deeply influenced by mathematics, much of my thinking is shaped by applying mathematical analogies to both work and life. However, it’s important to note that this essay is not intended to be mathematically accurate but is instead an intellectual exercise. As I outlined in the previous piece, while design is inherently creative and human-centered, employing frameworks allows us to abstract its evolution, enabling a clearer understanding of how design must change as needs evolve. This collaboration with AI, viewed through Heidegger’s lens, is not meant to suggest that design is a mechanical or purely technical process. Instead, it probes how both human creativity and artificial intelligence—like Heidegger’s notion of tools—work together to shape our experience, while the essential human desire for aesthetics and delight remains central to our relationship with technology.

The structure of needs and interfaces

Let $N$ be a set of needs, where each element represents a specific user or business need. Similarly, let $I$ be a set of interface elements, which consists of components, controls, and other features of the design system.

We define a function that maps needs to interface elements:

$$f: N \to I$$

where each need $n_i \in N$ is mapped to an interface element $i_j \in I$. This function represents the translation of user and business needs into design elements. The function $f$ need not be bijective, meaning not every need corresponds to a single interface element, nor does each interface element satisfy only one need.

Set definitions

Needs set: $N = { n_1, n_2, \dots, n_m }$, where each $n_i$​ represents a specific need (e.g., usability, accessibility, compliance).

Interface Set: $I = { i_1, i_2, \dots, i_n }$, where each $i_j$ represents a specific interface element (e.g., buttons, input fields, icons).

Mapping needs to interface

The mapping function $f$ can be extended to handle situations where multiple needs map to the same interface element or a single need maps to multiple elements. In this case, we can define:

$$f: N \to 2^I$$

where $2^I$ represents the power set of $I$, meaning each need can map to a subset of interface elements. This allows for more flexibility, acknowledging that complex needs may require multiple interface components to address them.

If \( N = \{n_1, n_2\} \) and \( I = \{i_1, i_2, i_3\} \), then \( 2^I \) includes:

\[ 2^I = \{\emptyset, \{i_1\}, \{i_2\}, \{i_3\}, \{i_1, i_2\}, \{i_1, i_3\}, \{i_2, i_3\}, \{i_1, i_2, i_3\}\} \]

Now, \( f(n_1) \) could map to \( \{i_1, i_3\} \), which is one element in \( 2^I \). Similarly, \( f(n_2) \) could map to \( \{i_2\} \).

• Each need $n \in N$ maps to one subset of interface elements from $I$, even if that subset contains multiple elements.
• Therefore, the mapping is a function, because each input (need) corresponds to exactly one output (a subset of interfaces), even though the output itself may contain multiple elements.

Stagnant Interface

In a stagnant interface, there is no evolution of $N$ or $I$. The function $f$ remains constant:

$$f(n_i) = i_j \quad \forall n_i \in N$$

This situation arises when user needs are fully met by the existing interface, and no additional updates are necessary. Over time, while such interfaces may look outdated, they still serve their basic purpose. Examples include legacy systems like Craigslist or Hacker News.

Progressive Change

In most cases, design needs evolve gradually. Let’s introduce the concept of incremental needs $N_{\text{incr}} \subset N$, which represent small changes in user behavior, business policies, or technology. These changes result in incremental modifications to the interface set $I_{\text{incr}} \subset I$

We define a differential mapping to represent these small changes over time:

$$\frac{df(n)}{dt} = \frac{\Delta I}{\Delta t}$$

where $\frac{df(n)}{dt}$​ represents the rate of change in interface elements required to address incremental changes in needs over time. The goal of incremental design is to maintain usability while minimizing disruption to the interface.

Evolution

Over longer periods, substantial changes in needs occur due to shifts in technology, user demographics, or business models. We represent these as substantial needs $N_\text{subst}$​ and their corresponding substantial interface changes $I_\text{subst}$​. The mapping function $f$ evolves into a new function, which we denote as $f′$:

$$f': N_\text{subst} \to I_\text{subst}$$

In this scenario, both the set of needs and the interface undergo significant transformations. An example is the evolution of Netflix, which transitioned from a DVD rental service to a streaming platform, necessitating a completely new set of interfaces to support the new business model.

Design Debt

Design debt occurs when the interface $I$ does not evolve in sync with the changing set of needs $N$. Over time, the mismatch between $N$ and $I$ creates inefficiencies, bloating the interface with redundant or obsolete elements.

We can define design debt mathematically as the difference between the ideal set of interface elements $I_\text{ideal}$​ and the actual set of interface elements $I_\text{actual}$​:

$$\text{Design Debt} = I_\text{actual} - I_\text{ideal}$$

Where:

• $I_\text{ideal} = f'(N)$, the optimal set of interface elements that perfectly satisfies the current needs.
• $I_\text{actual}$ is the existing set of interface elements, which may include obsolete components.

As design debt increases, the cardinality of the difference set $|I_\text{actual} - I_\text{ideal}|$ grows, indicating the extent to which the interface has diverged from its optimal form. This leads to a bloated interface that hampers usability.

Temporal Decoupling - The growth of design debt is exacerbated by temporal decoupling, where needs evolve $(N_\text{subst}​)$ but the interface remains static $(I)$. In enterprise systems, this leads to a legacy UI, where interface elements become disconnected from current user needs.

Redesign and Innovation

Redesign becomes necessary when the set of needs NNN and the set of interface elements III become so misaligned that incremental changes can no longer suffice. In this case, we introduce the concept of a complete remapping:

$$f_{\text{redesign}}: N_\text{new} \to I_\text{new}$$

Here, redesign represents a new mapping that starts afresh to address unfulfilled needs and resolve accumulated design debt. Redesign should not be confused with evolution, which is an ongoing process. Instead, redesign occurs when the previous interface becomes obsolete and cannot accommodate evolving needs.

Innovation as Temporal Decoupling

Occasionally, an innovative interface creates a positive temporal decoupling, where the interface anticipates future needs. This situation represents a surplus of functionality, where the interface $I$ exceeds current needs $N$, and future needs will catch up to the interface over time. This is mathematically represented as:

$$I > N \quad \text{(where the current interface serves future needs)}$$

This form of positive decoupling allows companies to stay ahead of the competition by introducing latent needs that users didn’t initially know they had.

Conclusion

By introducing mathematical rigor to the relationship between needs and interfaces, we can model design processes with greater clarity. Design debt, incremental changes, and redesign can all be quantified and understood through this framework. While abstract, these mathematical constructs provide a systematic approach to design evolution, allowing us to better manage the complexities of user needs, interface elements, and the inevitable bloat of enterprise systems.

In this framework, optimization becomes a key goal—seeking the most efficient interface that balances current needs with future evolution, all while minimizing design debt.